STEP3
小石の数理にチャレンジ
ピタゴラス教団が研究した様々な数の間にはいろいろな不思議な関係が見つかりました。古代ギリシアの人々の考え方で数の性質について考え、「数の面白さ」を感じてみましょう。「小石の数理」を使って問題にもチャレンジしてみましょう。
HOME > すうがく教室 > ピタゴラスと数 目次 > Step3
小石を並べて数のグループ分けができるなんてゲームみたいだね。ピタゴラス教団の人たちが興味を持ったっていうのもわかる気がしてきたぞ。
確かに！小石を並べて整った形になったら何か意味がありそうだもんね。宇宙の調和や秩序を象徴する神聖なものという考えにつながったのかな。
図形で分類した数のグループにはいろいろな不思議な性質がわかっておるぞ。実際にどんな形になるか確認しながら見てみよう。
三角数と長方形数の関係
三角数と長方形数の関係を調べてみましょう。下の図は4番目の三角数とこれをひっくり返したものを合わせた形です。三角形を二つ合わせると4×5の長方形になります。つまり、縦の個数より横の個数が一個だけ大きい長方形になります。
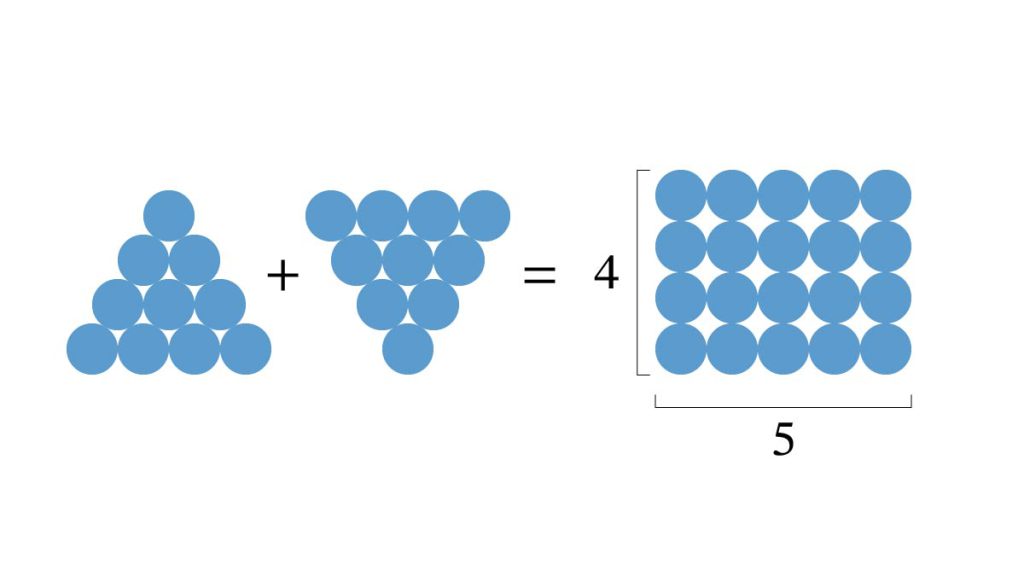
小石の数を数えてみましょう。長方形の小石の数は 4 × 5 で20個です。三角形の小石の数はその半分なので10個です。
このような法則に気づくと、n番目の三角数は、縦n、横(n+1)の長方形の半分になることがわかり、n番目の三角数(1+2+…+n)を簡単に求めることができます。
えっと、三角数というのは小石を1個、2個…と順番に並べて足した数だったよね。4番目の三角数というのは1+2+3+4ということか。
1+2+3+4と一つずつ足していってもいいけど、三角形を逆さまにしてくっつけて、長方形にして考えれば簡単に求める事ができますね。
そうじゃ。n番目の三角数の二つ合わせると、縦の個数がn、横はn+1の長方形になるという規則じゃな。もう一つ三角数に関する面白い規則を紹介しよう。
三角数と正方形数の関係
三角数は正方形数（平方数）とも関係があります。隣り合う2つの三角数の和は正方形数になります。
具体的に見てみましょう。三角数を小さい方から順番に並べると以下のようになります。
1, 3, 6, 10, 15 …
この三角数の中で3番目の「6」と4番目の「10」 は下の図のように正方形に並べることができます。小石の個数は 4 × 4 ( = 42 ) で16個となります。
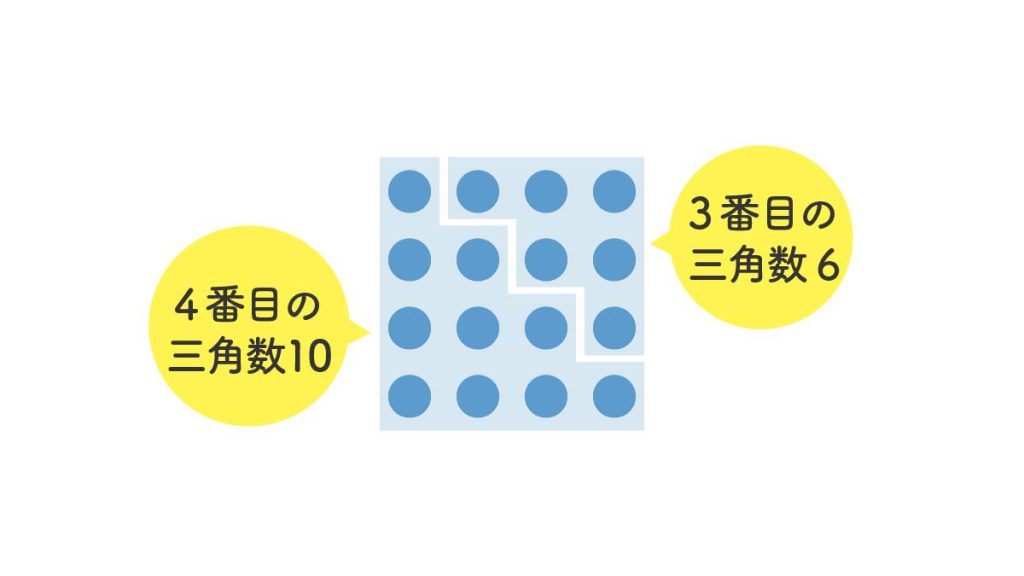
ほんとだ。小石の形が正方形になっている！ピタッとハマってパズルみたいだね。
現在は上で示した内容を式を使うことでシンプルに表すことができる。みんなにとっては式を使った証明の方が馴染みがあるかもしれんな。今回は式の証明は省略してもう一つ別の規則を紹介するぞ。
奇数の和と正方形数の関係
1から始まる連続する奇数の和を考えてみましょう。小石を並べて考えます。1,3,5,7を下の図のように並べます。
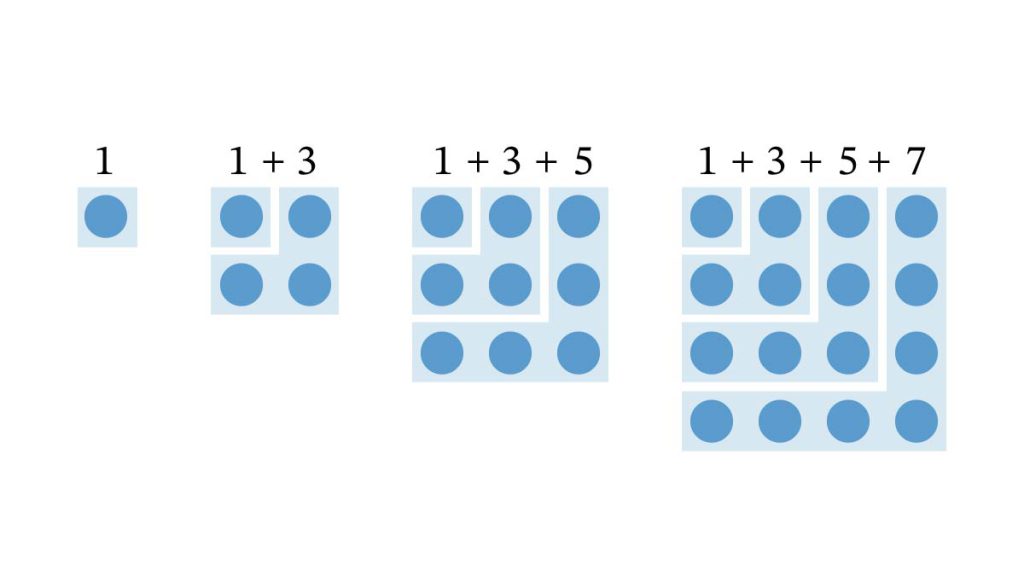
このように並べると連続する奇数の和は正方形数（平方数）になっていることが一目瞭然でわかります。
図に現れる Ｌ字型、あるいはLを反転した図形はグノモンと呼ばれ、ギリシアの数学ではたびたび現れます。グノモンとは、日時計を簡略化したL字形の時計で、突起部の影の長さで時刻を測る器具です。
うんうん、わかってきたかも！奇数を順番に足していったらL字が追加されて正方形が大きくなるんですね！小石で並べると、このルールがわかりやすいね。
古代ギリシアの人たちは小石を並べて形を作り、その形から数に関する不思議な性質を読み取っていたんじゃな。さて、これまで見てきた内容を簡単なクイズにするからチャレンジしてみよう。
長方形数 クイズ
古代ギリシアでは長方形に並べられる数を長方形数と呼んでいました。今の言葉でいうと、長方形数とは合成数のことです。長方形数でない数を素数といいます。
Q1
小石を並べて確かめてみよう！
14個の小石は長方形に並べられるかな？
答えを見る
A
長方形に並べられる（14は合成数）
Q2
小石を並べて確かめてみよう！
15個の小石は長方形に並べられるかな？
答えを見る
A
長方形に並べられる（15は合成数）
奇数の和と正方形数 クイズ
1個、3個、５個、7個の小石をグノモン（L字型）の形に並べていくと正方形になります。連続する奇数の和(1+3+5+7)は正方形数になることがわかりました。
Q1
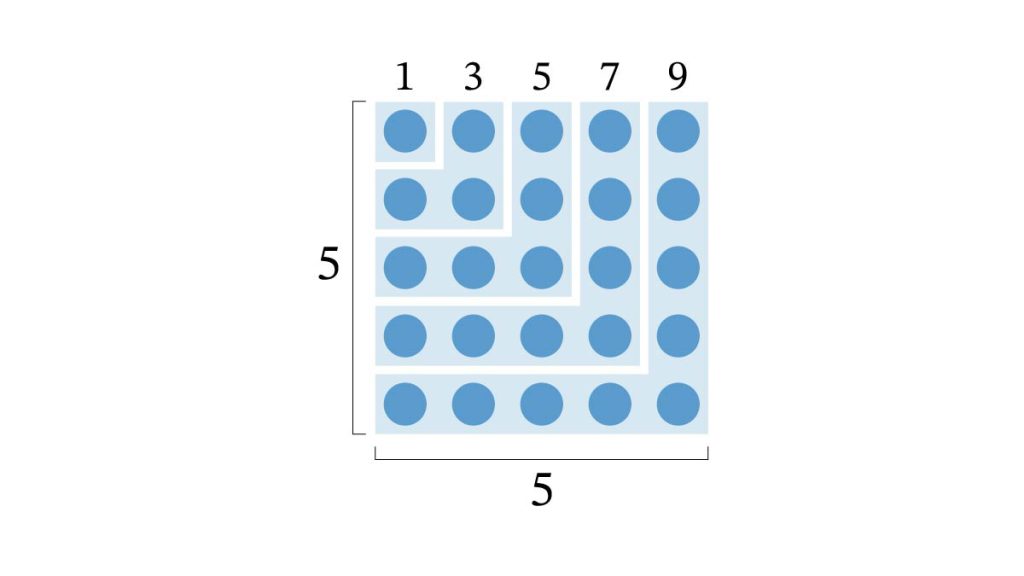
1から9までの奇数の和はいくつになるかな？
小石をグノモンの形に並べて、正方形を作って考えてみよう。
答えを見る
A
25
1個、3個、5個、7個、9個の小石を上の図のように並べると、5 × 5 =25の正方形に並べられます。したがって1から9までの奇数の和 （1+3+5+7+9）は25になります。
Q2
1から13までの奇数の和はいくつになるかな？
小石をグノモンの形に並べて、正方形を作って考えてみよう。
答えを見る
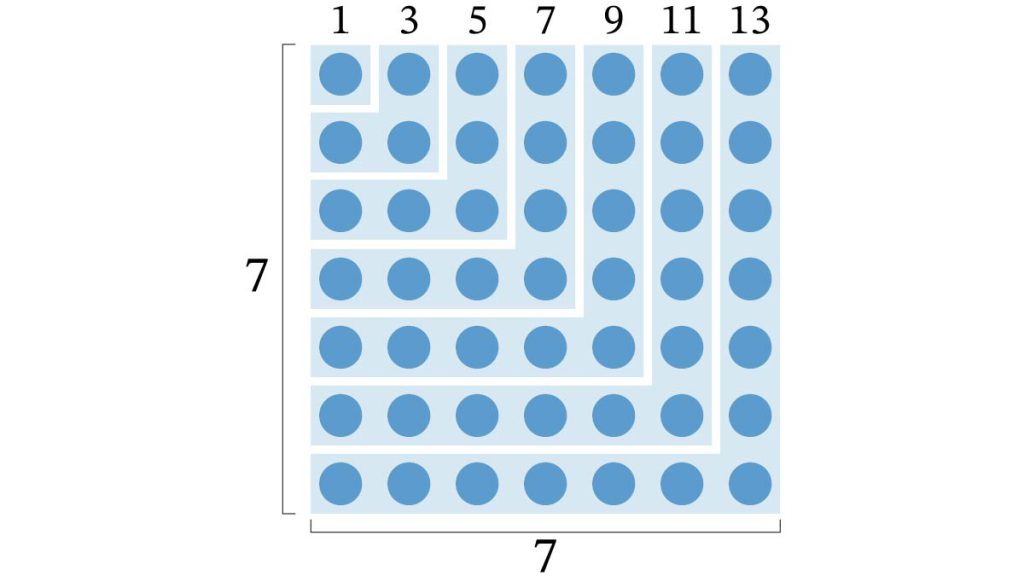
A
49
1個、3個、… 13個の小石を上の図のように並べると、7 × 7 =49の正方形に並べられます。したがって1から13までの奇数の和 （1+3+5+7+9+11+13）は49になります。
三角数クイズ
小石を三角形に並べた三角数を二つ合わせると長方形になります。n番目の三角数は、縦n、横(n+1)の長方形の半分になることがわかりました。
Q
7番目の三角数はいくつ？
ヒント：まずは1個、2個…7個の小石を三角形に並べてみよう
答えを見る
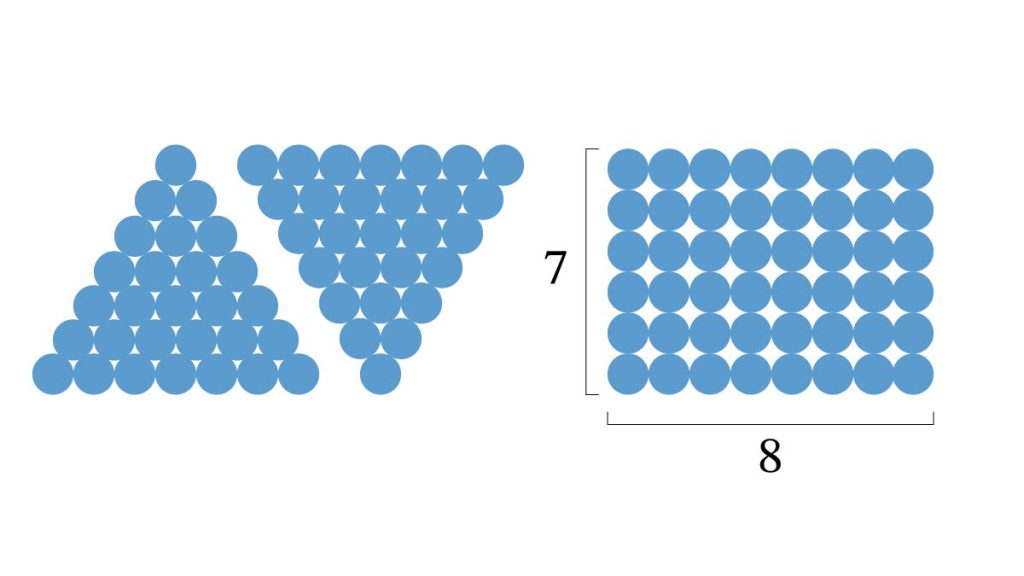
A
28
1個、2個…7個の小石 を上の図（左）のように三角形に並べます。三角形をひっくり返して合わせると縦7、横8の長方形になります。
長方形の小石の数は 7 × 8 = 56。 三角数はこの半分なので答えは28になります。
『ピタゴラスと数 -万物は数である-』はこれで終了です！
ピタゴラスや古代ギリシアの人たちがどんなふうに数を分類していたのか、少しイメージできたかな？
チャプター
Step1 . ピタゴラスの定理と古代ギリシア
Step2. ピタゴラスが分類した数
Step3. 小石の数理にチャレンジ
– 三角数と長方形数の関係
– 三角数と正方形数の関係
– 奇数の和と正方形数の関係
– 小石の数理クイズ
キャラクター紹介
ポゥじい
Pou-Ji
フクロウの博士。数学のことならなんでも知っているけど、ちょっぴりうっかり屋さん。口ぐせは「学ぶって最高に楽しいんじゃよ！」
スウカ
数花
数学が得意な中学生。しっかり者で好奇心旺盛。歴史の知識も豊富でクイズが得意。数学の謎を見つけると目をキラキラさせる。時々鋭い指摘をする。口ぐせは「うんうん、わかってきたかも！」
カズオ
数男
数学はちょっと苦手な中学生。最近数学の面白さに気づいて学び始めた。のんびりマイペース。じっくり考える力はピカイチ。口ぐせは「よくわかんないけど、なんかおもしろそう！」
関連するレッスン
ー 準備中 ー