万物は数である

「万物の根源は数である」…ピタゴラスはこの世界のすべてのものは「数」でできていて、「数」で説明できると考えました。

数には神秘的な力があると信じていて、一つずつの数にいろいろな意味を持たせ、世界（あるいは宇宙）に生じるさまざまなことがらに数を結び付けました。一つ一つの数は独自の個性を持っていると考えたのです。

ピタゴラス教団では数の持つ性質を研究し、その性質によってグループ分けしました。偶数や奇数、平方数や立方数、合成数や素数、などです。これらの数の間にはいろいろな不思議な関係が見つかりました。

数の分類1 – 偶数と奇数

四則演算（たし算・ひき算・かけ算・わり算）や x などの便利な表記方法がなかったピタゴラスの時代を想像してみましょう。“偶数”や“奇数”はどのように表現されていたのでしょうか。四則演算の概念が確立されていないので、「2で割り切れる数を偶数と呼ぶ」ということはできません。現代ではお馴染みの表現方法“2k”などの表記も使えません。

ピタゴラスは数を『小石を並べてできる形』で分類しました。2列に並べることができる数を偶数、列に並べると1つ余る数を奇数と呼んだのです。

• 2列にきれいに並べられる数は「偶数」
• 2列に並べると1つ余る数は「奇数」

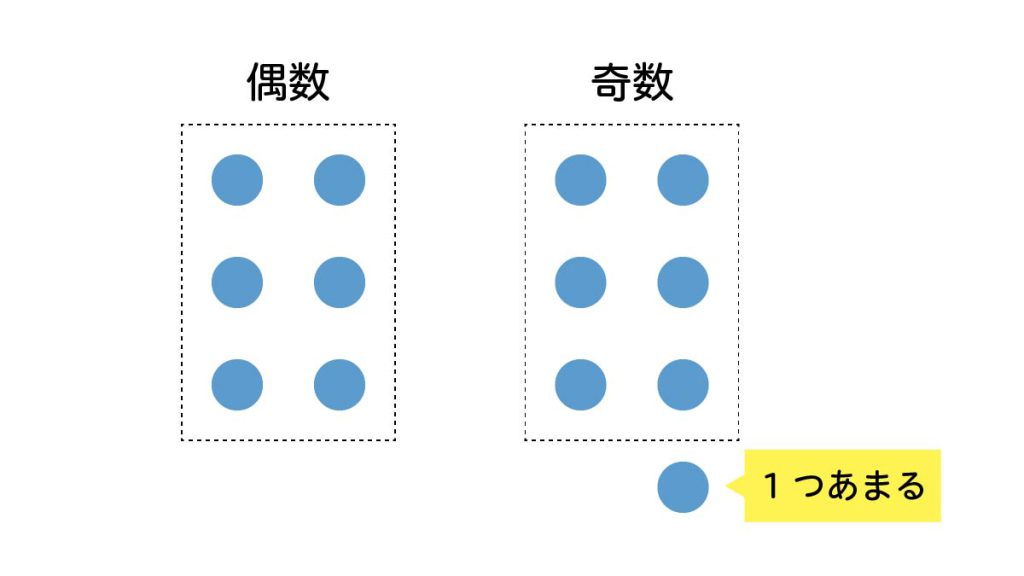
このように、見た目や形に基づいて数を分類し、新しい言葉（概念）を作り出すことが、当時の数学における「理論の始まり」だったのです。

数の分類2 – 長方形数

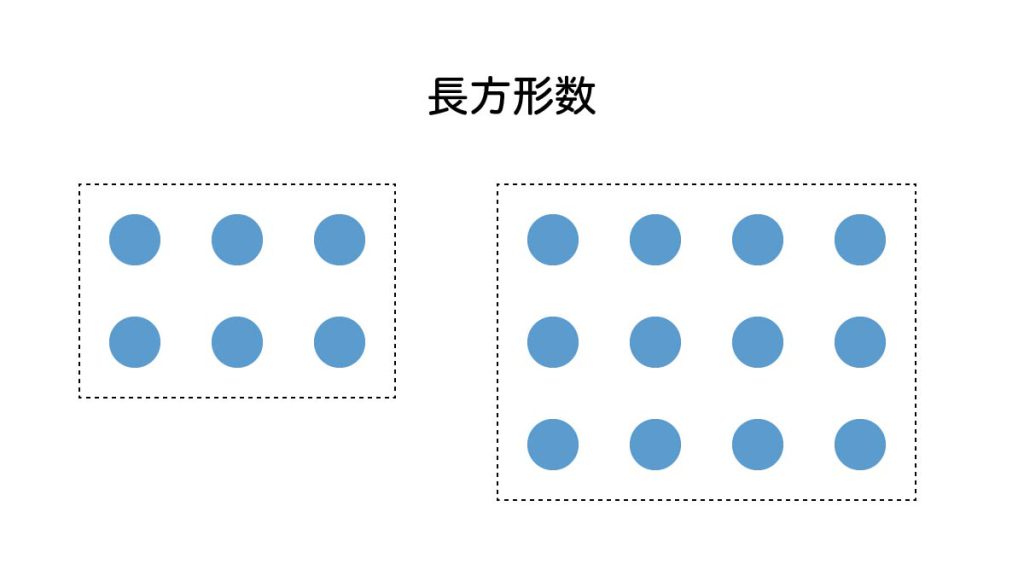
長方形に並べられる数を古代ギリシアでは長方形数と呼んでいました。ただし1列は長方形とは認めません。例えば6、12などは長方形数です。今の言葉でいうと、長方形数とは合成数のことです。長方形数でない数を素数といいます。2、3、5などは長方形数に並べることができないので素数です。

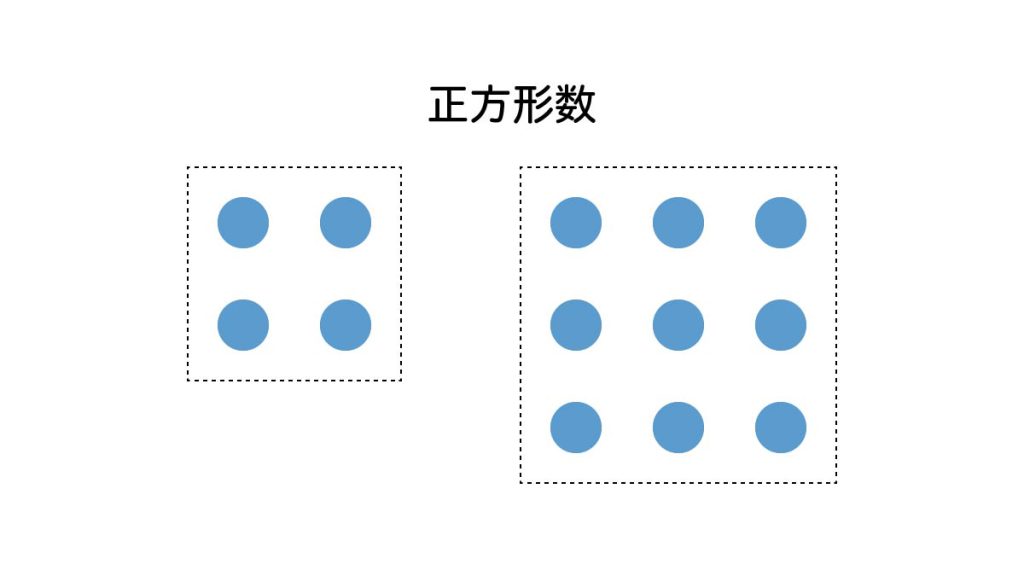
正方形に並べることができる数を正方形数といいます。今の言葉でいうと、正方形数とは平方数のことです。

ギリシアでは形で数を分類しましたが、現在の私たちは数を、掛け算を使って分類します。1以外の2つの数の積として表される数を合成数、ある数の平方（2乗）で表される数を平方数と呼んでいます。たとえば、ある数 a が2つの数 b と c の積で表されるなら、すなわち a＝b×c (b≠1, c≠1) なら、a は b と c から「合成される」から今では合成数と呼ばれ、ギリシア時代では、a個の小石は、縦 b、横 c の長方形に並べられるから長方形数と呼ばれたのです。正方形数と平方数の関係も同様で、同じ概念を表します。 

数の分類3 – 三角数

古代ギリシアでは、小石を小さい数から順に並べて足し合わせたときにできる、正三角形の形をした数を「三角数」と呼んでいました。

• 1番目の三角数 → 1
• 2番目の三角数 → 1 + 2 = 3
• 3番目の三角数 → 1 + 2 + 3 = 6
• 4番目の三角数 → 1 + 2 + 3 + 4 = 10
• 5番目の三角数 → 1 + 2 + 3 + 4 + 5 = 15

というように、小石の数を順番に足していった小石の総数（1, 3, 6, 10, 15 …）が三角数になります。

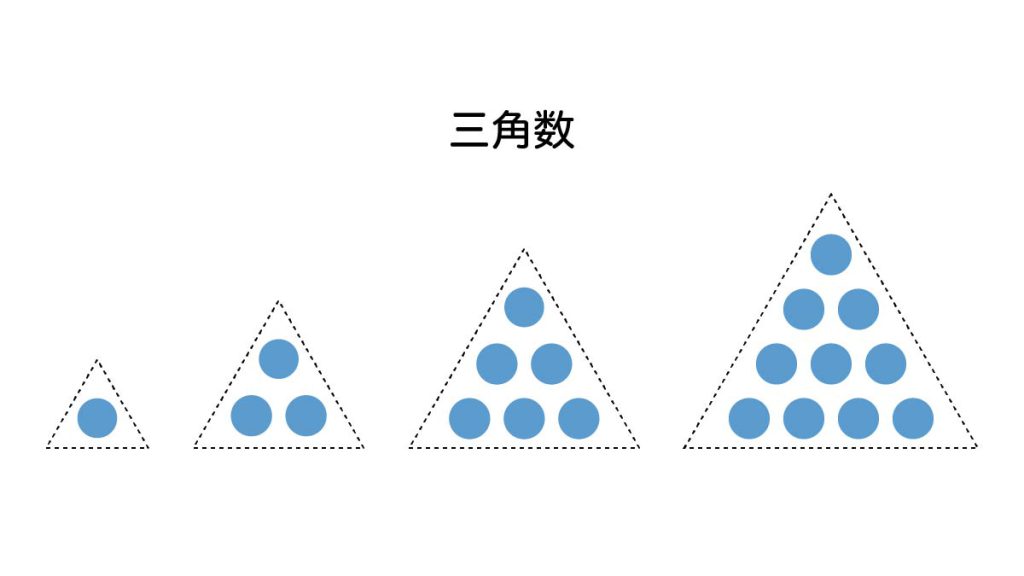
ピタゴラス教団にとって、数は宇宙の基本的な構成要素と考えられていました。特に三角数は、完全性や調和の象徴とされ、宇宙や音楽の基礎構造と結びつけて考えられました。10個の小石を三角形に並べた形（4番目の三角数）はピタゴラス教団では「テトラクテュス（tetraktys）」と呼ばれ、シンボルマークとされていました。