
無理数とは何者? ― 終わりなく続く不思議な数

学校で、√2 は『無理数』って習ったけど、無理数ってどういう数なのかな? 有理数とは何が違うの? 見分けるコツがあれば知りたいな。

Q. 「無理数」と「有理数」の違いとは?
私たちは普段、1、2、3といった整数や、0.5のような小数、1/2のような分数を「数」として当たり前に使っています。大昔の人々にとって「数」とは整数(物の個数)のことでした。しかし数学の発展と共に、これまでのルールがどうしても通用しない、不思議な数が存在することがわかってきました。
数字の羅列がどこまでも続き、正体が掴みきれない――。そんな「無理数」とは、一体どのような性質を持った数なのでしょうか?
A. 「分数(整数の比)」で表せるかどうかが、分類の決め手です。
数を大きく2つのグループに分けて考えるとき、「分数の形」で表せるかどうかが決め手となります。
有理数:分数で表せる数。例えば0.1なら1/10、0.333…なら1/3というよう分数の形に変換できる数を、有理数といいます。
無理数:分数の形(整数の比)で表せない数。最大の特徴は、小数にしたときに「同じ数字の並びを繰り返さず、無限に続いていく」という点です。
代表的な無理数には次のようなものがあります。
√2: 1.41421356…
円周率π: 3.14159265…
この循環せずに終わりなく続く数こそが、無理数の正体です。
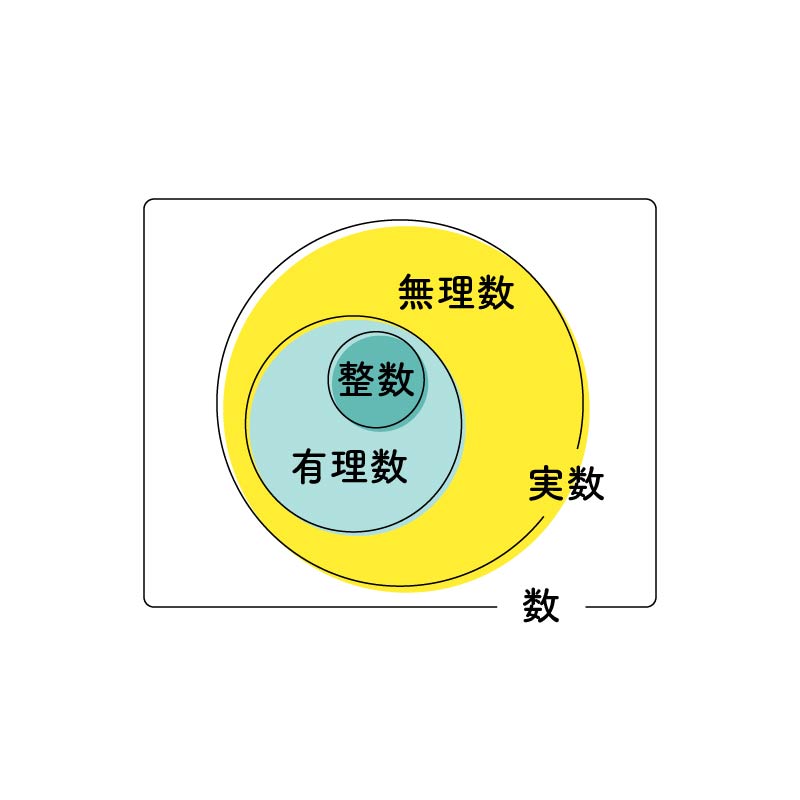

なるほど、分数にできるかどうかがポイントなんだね! 0.333…みたいにずっと続く数でも、1/3っていう形に収まれば有理数。無理数は分数には収まらず、バラバラな数字が永遠に続いていくんだね。

ピタゴラス教団の禁忌?無理数とヒッパソス事件とは
古代ギリシアのピタゴラス教団では「万物は数でできている」という強い信念を持っていました。世界はすべて、音階のように美しい整数の比で説明できると信じていたのです。
ところが、そんな彼らの完璧な世界を揺るがす「例外」が見つかってしまいます。それは、あまりにも身近な「正方形の対角線」でした。
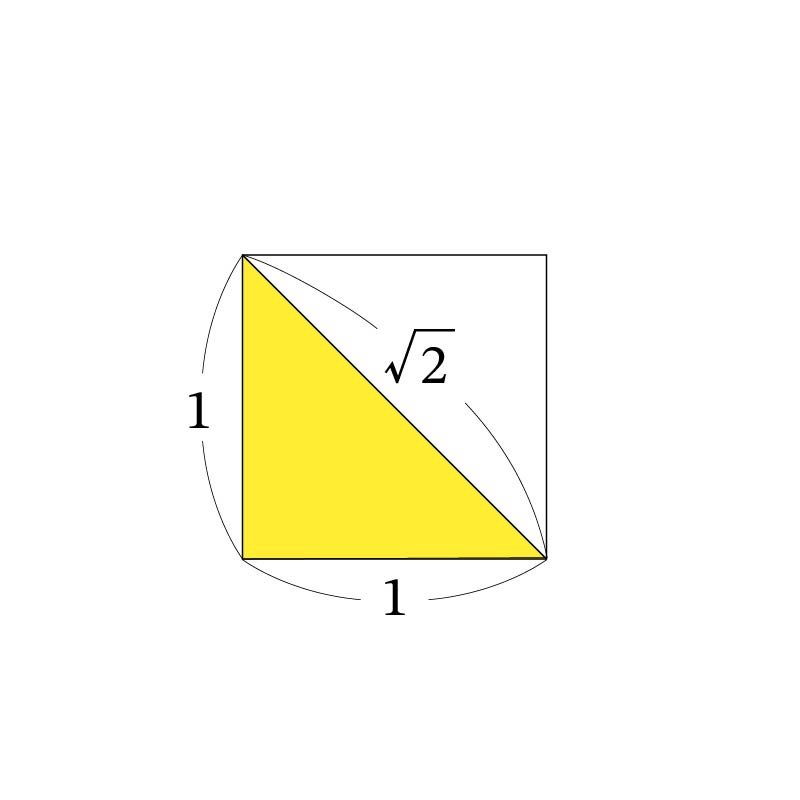
一辺の長さが1の正方形の対角線を測ると、その長さは √2 となります。この √2 は、どんなに工夫しても整数の比(分数)で表すことができませんでした。
教団にとって、分数で表せない数の存在は、世界の秩序を壊す「あってはならない禁忌」でした。この事実は教団内で秘中の秘とされました。ある時、団員のヒッパソスがこの発見を口外してしまいます。この事が明るみに出て、教団の怒りに触れたヒッパソスは、船から海へ突き落とされた……という恐ろしい逸話まで残っています。
「無理数」は、命を懸けてまで隠し通そうとされた、不合理な怪物だったという象徴的なエピソードです。

無理数の発見は、古代ギリシアの人たちにとって、どんな意味があったのかな…。当時の人たちの「数」に対する考え方は今の私たちの感覚とは少し違ったのかもしれないね。

広がり続ける「数」の世界 ― 実数への長い道のり
古代において「数」とは、羊の数や道具の個数を数えるための「1、2、3…」という自然数だけを指していました。当時の人々にとって、数は目に見えるものを数えるための道具だったのです。
しかし、人類の活動が広がり、思考が深まるにつれて、数の世界は少しずつその姿を変えていきました。
・0や負の数:「ない」ことや「足りない」ことを表す
・分数や小数:1より小さい数
・無理数:分数では表せない数
私たちは現在、「無理数は有理数でない実数である」と簡単に定義できます。けれども、そのためにはまず「実数とは何か」が明確でなければなりません。しかし実数が厳密に定義されたのは、19世紀になってからのことです。今では当たり前に思えるこの数の分類も、実は人類が何千年もかけて築き上げてきたものなのです。

わしらが今、教科書でさらりと習う一行の定義の裏には、実は何千年もかけて少しずつ姿を変えてきた長い歴史があるのじゃよ。数学とは、人類がこの世界をどうにかして理解しようともがいてきた、熱い『冒険の記録』なんじゃな。
もっと深く知りたい方へ

私たちは今、「無理数」を当たり前に受け入れています。しかし、古代ギリシアの人々が見ていた「数の世界」とは一体どのようなものだったのでしょうか?
電子書籍 ポゥじいとめぐる「数」の旅 『古代ギリシアの数2 ー 無理数は本当に発見されていたのか?』では、今回ご紹介した無理数の事件の話を入り口に、古代ギリシアの人々が数や図形の世界を切り開いていった知のプロセスを、ポゥじいたちと一緒に体験していきます。
教科書の一行では語り尽くせない、数学という名の冒険の続きを、ぜひ本書で味わってみてください。
