
正多面体は5つしかないの?「プラトン立体」の秘密

正三角形や正方形って、どこまでも角を増やしていけるよね。だったら、それで作る『正多面体』も、正六面体、正七面体……って、いくらでも種類があるんじゃないの?えっ、世界に5つしかないって本当なのかな?

Q. 正多面体は5つしか存在しないの?
「正多角形」なら、正五角形、正六角形、正百角形……と、角の数を増やすことで無限に種類を作ることができます。
それなら、すべての面が同じ正多角形でできている「正多面体」も、同じようにいくらでも種類がありそうに思えませんか?
実際のところ、この世界には一体何種類の正多面体があるのでしょうか。
A. 正多面体はたったの「5種類」しか存在しません。
どんなに角を増やそうとしても、どんなに工夫して組み立てようとしても、すべての面が同じ形で、どの頂点にも同じ数の面が集まる「正多面体」は、この宇宙に5つだけなのです。
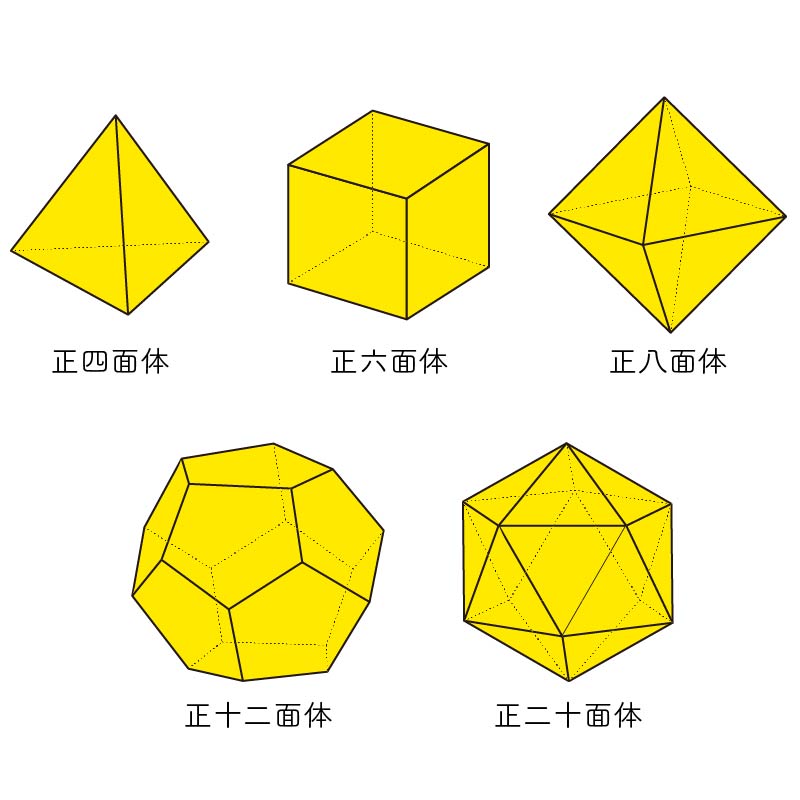
その5つとは、正四面体、正六面体(立方体)、正八面体、正十二面体、正二十面体です。
これはこの世界の「空間のルール」によって決まっていることなのです。古代ギリシアの数学者ユークリッドは、その著書『原論』の最後を、この「正多面体は5つしかない」という証明で締めくくっています。
なぜ6つ目は作れないのか? その不思議な理由は、次に紹介する「角度のパズル」に隠されています。

たくさん作れそうなのに、「5つだけ」って決まっているなんて……。なんだか、選ばれた特別な形って感じがするね!

正多面体が5つしかないことの証明
面白いことに、世の中に正多面体は5つしか存在しません。
ユークリッドは『原論』の最後の巻で、「正多面体は5 種類しか存在しない」ことを
見事に証明しています。一つの頂点に集まる正多角形の角度の合計が360 度を超えると、もはや立体として閉じることができなくなります。つまり、平面になってしまうのです。
たとえば正三角形では、1 つの頂点に3枚集めれば正4 面体、4 枚集めれば正8 面体、5 枚集めれば正20 面体ができます。ところが、6 枚になると、角度の合計が 60 × 6 = 360 度となってしまい、平面になってしまいます。よって立体としては成立しないのです。
正5 角形も同じで、12 枚で正12 面体が限界です。それ以上の多角形 ―― たとえば正6 角形や正7 角形 ―― では、立体にはなりません。

なるほど!図形を増やしすぎると、ふくらむ余裕がなくなってペタンコになっちゃうんだね。5つしかないのは、空間のスキマを埋めるための『絶妙なバランス』の結果なんだ!

古代ギリシアの哲学者プラトンの考え:宇宙の4大元素
古代ギリシアの哲学者プラトンはこの5つの正多面体に宇宙の4 大元素と、空間そのものを割り当てました。
火は正4 面体、空気は正8 面体、土は正6 面体、水は正20 面体、そしてエーテル(宇宙に充満する神秘的な元素)、あるいは宇宙空間には正12 面体をあてがいました。あくまで哲学的な象徴ですが、形と意味とを結びつける想像力こそが、当時のギリシア思想の粋とも言えます。

プラトンたちは、この5つの形こそが「宇宙を形作る究極のパーツ」だと信じておったんじゃ。「美しい形には、世界を解き明かす鍵がある」と考えた彼らの情熱は、今の科学にも通じるものがあるのう。
たった5つしかない、完成された美しさ。次にサイコロを振る時は、その形に秘められた古代の知恵を思い出してみておくれ。
もっと深く知りたい方へ

「形」の中に宇宙の真理を見出そうとした古代ギリシアの人々。彼らにとって数学は、単なる計算ではなく、世界を読み解くための「鍵」そのものでした。
電子書籍 ポゥじいとめぐる「数」の旅 『古代ギリシアの数1 ー 数学はこうして生まれた』では、今回ご紹介した正多面体の神秘や、古代ギリシアの数学をさらに詳しく解説しています。
「数学の背後にある物語を知りたい」というあなたに、ぜひ読んでほしい一冊です。知的好奇心を刺激する冒険の続きを、本の中で楽しんでみませんか?
