「指数関数」って何？倍々に増える不思議

「1つが2つに、2つが4つに……」と、何かがどんどん増えていくお話を聞いたことはありませんか？ 最初はたった「1」でも、気づけば想像もできないほど巨大な数になっている。そんな「爆発的な成長」の裏に隠れているのが「指数関数」です。

一見、現代のコンピュータのための数学に思えますが、実は古代の人々もこの不思議な数に魅了されていました。まずはその基本をのぞいてみましょう。

---

A. 「倍、倍、倍」と、雪だるま式に増えていく数のことです。

最初は小さくても、ある地点から一気に加速して大きくなる。この「増え方のルール」が、指数関数の正体です。実際に増えていく様子を見てみましょう。

1 → 2 → 4 → 8 → 16 → 32 → 64 → 128 → 256 → 512 → 1024……

たった10回繰り返すだけで、なんと最初の1000倍以上に膨れ上がります。この急成長を計算式で表したものが「指数関数」であり、それを支えるのが「累乗（るいじょう）」という仕組みです。

右肩に乗った小さな数字（指数）は、「同じ数を何回掛け合わせるか」を教えてくれるサイン。たとえば「2¹⁰」は「2を10回掛ける」という意味で、これがスマホのデータ容量（ギガ、テラなど）の基礎にもなっています。

この指数的に増えていく数の「合計」を計算しようとすると、魔法のような便利な公式が見つかります。

「1から倍々に増やした数の合計は、最後の数を2倍して、そこから1を引いた数になる」

たとえば、1 + 2 + 4 + 8 + 16 を計算したいとき。普通に足すと大変ですが、このルールを使えば、最後の「16」を2倍した「32」から「1」を引くだけ。答えは「31」だと一瞬でわかります。数式で書くと次のようになります。

　　　　1 + 2 + 4 + … + 2ⁿ = 2ⁿ⁺¹ – 1　　

古代ギリシアの人たちは、現代のような便利な数式を持っていませんでしたが、この美しい関係を「言葉」や「形」として捉えていました。

どうしてそうなるのか？その理由は、次のトピックで『形』を使って解き明かしましょう。

古代ギリシアの数学は、計算よりも「図形の調和」を大切にしました。彼らがどのようにして「合計は2倍マイナス1になる」と理解していたのか、パズルのような証明を覗いてみましょう。

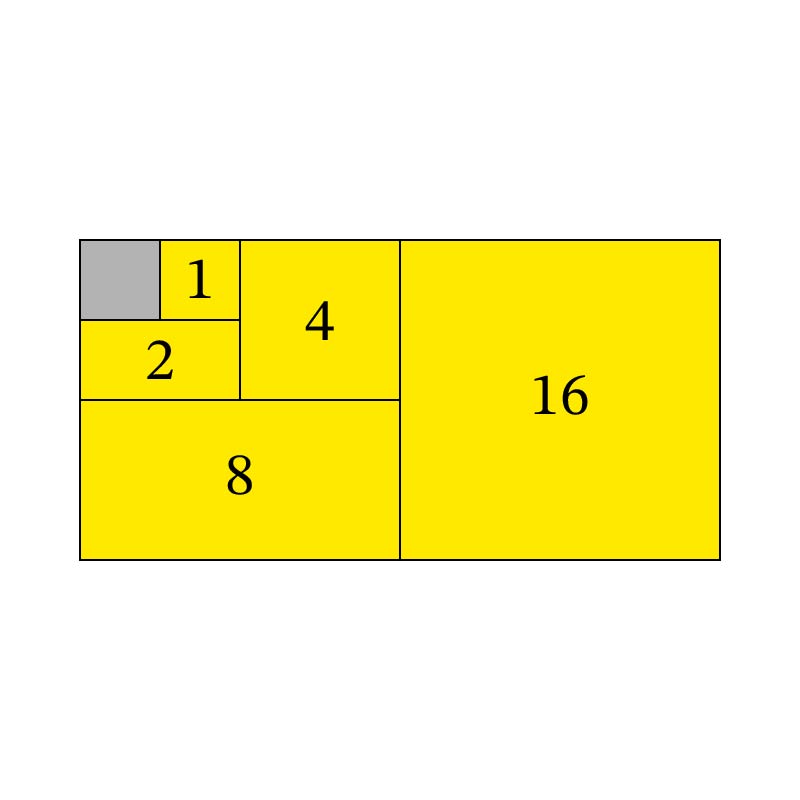
「1」をはめる： 隅にある空きスペースに「1」をはめ込むと、最初の「1」と合体して「2」の塊になります。

形を合体させる： できた「2」の塊は、下にある「2」のタイルとぴったり同じ大きさになり、合体すると「4」の正方形になります。

連鎖する合体： 合体した塊は、次々に隣のタイルと同じ大きさになります。最後には、一番大きなタイルと全く同じ塊がもうひとつできあがり、長方形が完成します。

最後に、最初に追加した「1」を差し引けば、元の合計が求められる――。式を使わずに「目で見て納得する」のがギリシア流の学び方です。