今日は数の歴史について考えてみよう。突然じゃが二人は数字を書くことはできるかな？

さすがに数字ぐらいは書けるよ！1、2、3…でしょ。いつも数学の計算式で使っているし、今はいろんなところに数字があふれているよね。

うん。数学の問題は難しいと思うことはあるけど、数字は小さい頃に書き方を覚えたし、当たり前に書けるものだと思うけど…。

そうじゃな。みんなは小さい頃から数字を使っておるから、簡単だと思うかもしれんな。しかし、この「数を表す方法」にたどりつくまでに人類はとても長い年月を費やしてきたのじゃよ。今回は数を表す「記数法」について学んでみよう。

まずは算用数字が生まれるずっと前、人類が数を扱いはじめた旧石器時代の頃を見てみよう。

え！旧石器時代の人たちって数を書いたりしていたんですか？今の数字と同じように書いていたのかな？

うーん、旧石器時代に数字なんていらないんじゃないかな？数学の授業があるわけじゃないし…。数字を使う必要なんてない気もするけど…。

へぇー。石器時代でも数を記録していたんだね！今の数字とはちょっと違うみたいだけど。

狩りで３匹の獲物を獲ったら3本の線を刻めば記録が残せるってことですね。数を線の本数で示せばいいから、見た目にもわかりやすいね。

数を表す「線刻」は、まだ文字がなかった時代に人類が「数える」「記録する」いう行為を始めた証拠として、非常に重要なものだと言える。その後、時を経て各地で数字が使われるようになるのじゃが…線刻と同じような表現をする古代の記数法を紹介しよう。

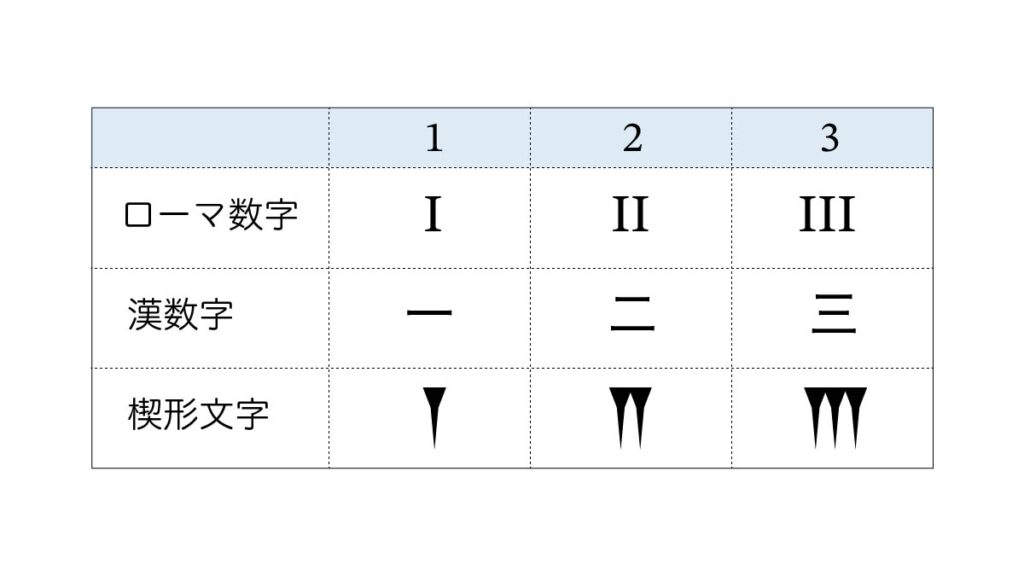
ほんとだ！みんな線を並べた形になってるね。1は一本、2は二本、3は三本だ。

使われていた場所や時代は違うけど、どれも「1 = 一本の線」と考えて数の分だけ並べたってことですね。

記数法の原点は「数を見える形にすること」じゃ。 最初は「線の本数」で表すのが直感的だったということじゃな。古代の数字には他にもいろいろあるぞ。次のステップでは古代エジプトの数字を調べてみよう！