
STEP1
三角形の合同・相似から学ぶ!図形の基本
図形の基本である三角形の合同条件・相似条件をわかりやすく整理します。さらに古代ギリシアにまでさかのぼり、幾何学の原点に触れてみましょう。数学が苦手でも楽しめる入門記事です。
HOME > すうがく教室 > ユークリッド幾何学 目次 > Step1


この前の授業で習った“三角形の合同条件”、私けっこう好きだな。三角形を比べるときに、ピタッと重なるっていう考え方がシンプルでわかりやすいんだよね。
へぇ〜、スウカはすぐ理解できたんだ。僕は条件をただ覚えるだけで精一杯だったよ。黒板に書かれた証明も追いかけるのがやっとで、気づいたら頭がいっぱいになってたんだ。


なるほどのう。実は“合同”というのは、幾何学で図形を正確に扱うためのとても大事な考え方なのじゃ。よし、ここで合同とは何かをあらためて整理してみようか。
三角形の合同条件
幾何学には、合同という重要な概念があります。ある図形 a が、移動したりひっくり返したりして図形 b とぴったり重なるとき、図形a は図形 b と合同であるといいます。
2つの三角形が合同かどうかを調べるのに、すべての辺や角を比べる必要はありません。ある条件を満たすだけで、「この2つの三角形は合同だ」と判断できるのです。これが三角形の合同条件です。
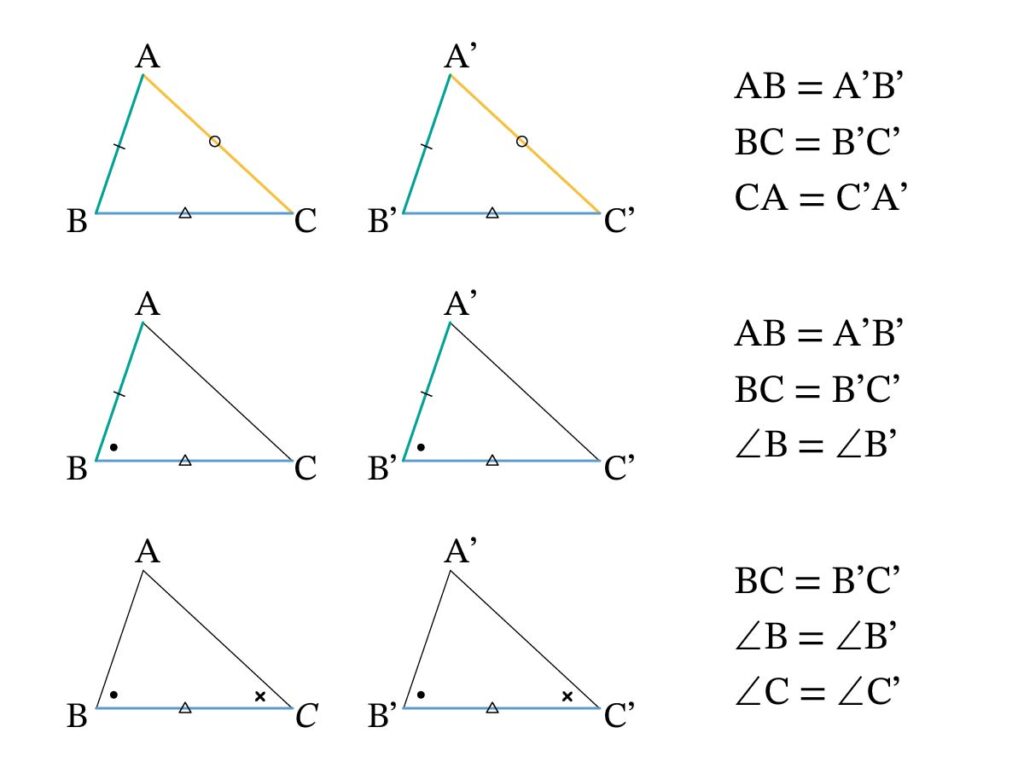
【 三角形の合同条件 】
(1) 3組の辺がそれぞれ等しい。
(2) 2組の辺とその間の角がそれぞれ等しい。
(3) 1辺とその両端の角がそれぞれ等しい。
三角形の相似条件
図形 a を拡大あるいは縮小することによって 図形 b にぴったり重ね合わせることができるとき、a と b は相似であるといいます。
2つの三角形が相似であるかどうかを調べるときも、ある条件を満たせば相似であることが判断できます。これが三角形の相似条件です。
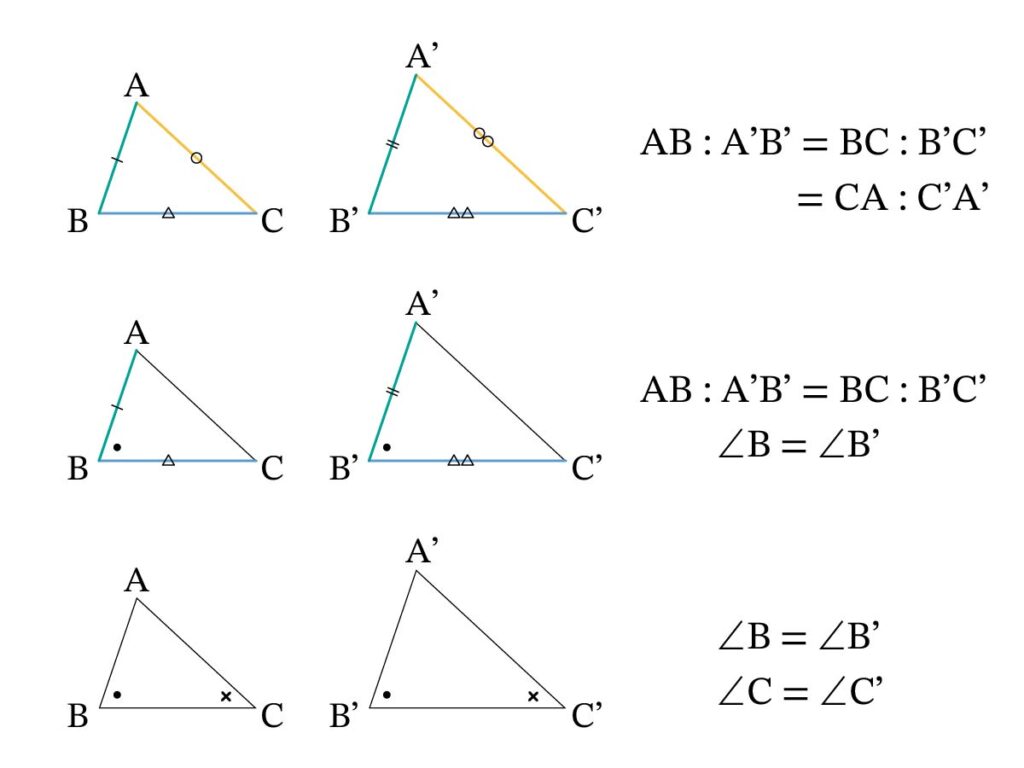
【三角形の相似条件】
(1) 3組の辺の比がすべて等しい
(2) 2組の辺の比とその間の角がそれぞれ等しい
(3) 2組の角がそれぞれ等しい

ふーん、合同は“大きさも形も同じ”で、相似は“大きさは違うけど形が同じ”なんだね。図形を見れば何となくわかるけど、条件だけ見るとちょっと複雑だなあ。
でも、図形を“どうやって比べるか”っていう考え方そのものが大事なんだと思う。形や大きさを論理的にとらえる視点が見えてきた感じ!


その気づきは鋭いのう。実は図形を“論理的に扱う”という姿勢こそ、古代ギリシアで大きく発展していったのじゃ。
幾何学と古代ギリシア
三角形の合同や相似の考え方は、図形の性質を正しく理解するための基本です。こうした“図形を論理でとらえる”姿勢は、古代ギリシアで大きく発展し、のちの学問の基礎となっていきました。
古代ギリシアの人たちは「図形がぴったりと重なる」という考え方を明確に定め、論理的に積み上げていきました。
点や線をどのように定義するのか、図形の性質をどう証明するのか――。その徹底した取り組みが、幾何学を体系的な学問へと押し上げたのです。

三角形 ABC と 三角形A’B’C’ が、それぞれの対応する辺や角で一致するなら、ぴったり重ね合わせることができる。これこそが古代ギリシア式の「等しい」という考え方の根幹なのじゃ。現代で学ぶ合同条件も、もとはこの発想に通じておる。図形の性質を正確に議論するために、重ね合わせ可能であることは極めて重要だったのじゃよ。
なるほど…。図形が“等しい”ことを厳密に考えることは古代ギリシアから始まっていたんですね。


へぇ〜、そんな考え方がもう古代ギリシアにあったなんて驚きだな。僕たちが授業で習ってる合同って、実はすごく歴史があるんですね!
そうなんじゃよ。その幾何学を体系としてまとめ上げたとされているのが――“ユークリッド”という人物なのじゃ。次のステップではユークリッドについて見てみようかのう。

\ Mathematicaでは電子書籍を販売しています /

ポゥじいとめぐる『数』の旅 シリーズ
ポゥじいとめぐる『数』の旅シリーズは、数学史を対話形式でわかりやすく解説した電子書籍です。中高生の学びから、大人の知的好奇心まで幅広く応える入門書。数の歴史や発見の物語を、やさしく楽しくお届けします。
チャプター
Step1 . 三角形の合同・相似から学ぶ!図形の基本
– 三角形の合同条件
– 三角形の相似条件
– 幾何学と古代ギリシア
Step2. 幾何学の父ユークリッドとは?
– ユークリッドとはどんな人?
– ユークリッドが活躍した時代
– 学問は何の役に立つ?
– 幾何学に王道なし
Step3. 幾何学の教科書 原論
– ユークリッドの原論とは?
– 原論の構成
– 古代ギリシアの量の捉え方
– ユークリッドクイズ
– 数学書クイズ
キャラクター紹介

ポゥじい
Pou-Ji
フクロウの博士。数学のことならなんでも知っているけど、ちょっぴりうっかり屋さん。口ぐせは「学ぶって最高に楽しいんじゃよ!」

スウカ
数花
数学が得意な中学生。しっかり者で好奇心旺盛。歴史の知識も豊富でクイズが得意。数学の謎を見つけると目をキラキラさせる。時々鋭い指摘をする。口ぐせは「うんうん、わかってきたかも!」

カズオ
数男
数学はちょっと苦手な中学生。最近数学の面白さに気づいて学び始めた。のんびりマイペース。じっくり考える力はピカイチ。口ぐせは「よくわかんないけど、なんかおもしろそう!」

